1 算法介绍

1.1 多项式乘法引入

1.1.1 多项式的两种表示方法

一般 $n$ 次多项式如公式（1）所示。多项式具有两种表示方法分别是系数表示法和点值表示法。

系数表示法：

任意多项式都可以通过一组系数所确定，而这组系数所组成的向量也叫做系数向量,通过系数向量表示一个多项的方式也叫做系数表示法。例如公式（1）中 $A(x)$ 的系数向量为：$\mathbf{a}=[a_0 ,a_1,\ldots,a_{n-1},a_n]$。

点值表示法：

对于一个已知的多项式例如公式（1）中的 $A(x)$ ，将 $x_i$ 代进去可以得到一个确定的值 $y_i$ ，如：$y_0=A(x_0)$ 。且可将 $(x_0,y_0)$ 看作是坐标系上的一个点。可将任意多（互不相等）的自变量 $( x_1,x_2,\ldots,x_{n-1}, x_n)$ 代入到 $A(x)$ 中，从而得到更多的点：$(x_1,y_1),(x_2,y_2),\ldots(x_n,y_n)$。通过 n+1 个不同点组成的点集 $P=\{(x_0,y_0),(x_1,y_1),\ldots,(x_n,y_n)\} $ ，唯一确定一个 n 次多项式，该方式也叫做多项式的点值表示法。

1.1.2 多项式乘法

已知两个多项式 $A(x)$ 和 $B(x)$，分别是 $n$ 次多项式和 m 次多项式。

公式（2）和公式（3）相乘得到一个最高为 $n+m$ 次的多项式 $C(x)$。系数向量：$\mathbf{c}=[c_0 ,c_1,\ldots,c_{m+n}]$。

系数乘法：

系数乘法，将两个多项式的系数相乘，系数相乘，如公式（5）所示。不难看出时间复杂为 $O(n^2)$。整理可得公式（6）。

点值乘法：

点值乘法只需将要将对应的纵坐标相乘即可，但是因为新得到的多项式次数更高，所以每个因子多项式都需要提供 $m+n+1$ 个点参与运算。时间复杂度为 $O(n)$。

小结

在计算多项式乘法时，点值表示的时间复杂度低。但是在计算系统中系数表示更加的常用。于是很自然的想到，在进行乘法时从系数表示转换到点值表示，使用点值表示法进行乘法运算，然后再转换为系数表示法。

但是很不幸的是，从系数表示转换到点值表示，以及点值表示到系数表示，这两个过程的时间复杂度均为 $O(n^2)$。

图1 多项式乘法总结图

1.1.3 转换优化

如果通过减少求值的点数可以较少计算时间。根据函数的奇偶性我们可以只求一半的点值，从而减少一半的计算量。这里为了方便表示设一个 $n-1$ 次的一般多项式，$n=2^a , a\in \mathbb{N}$。

将偶次项和奇数项分别组合：

对奇次项提取公因式 $x$:

化简为：

则我们可以取 $\frac{n}{2}$ 对相反数点，这样我们只需要计算一半的点值。

观察公式（7）不难发现，是将是将 $P(x)$ 拆成了两个规模为 $\frac{n}{2}$ 的 $P_e(x)$,$P_o(x）$。自然而然想到了递归执行。但是问题是相反数平方运算后所得结果均为正数，无法构造相反数对，无法实现递归。如果能一直保持相反数点对，那么时间复杂度可以表示为$T(n)=T(2n)+O(n)$ ，即时间复杂度为 $O(n\log n)$。

1.1.4 单位根（复平面）

既然实数域没有办法解决上面的问题，可以将起扩展到复平面。我们希望取一些点使其平方后的结果依然存在相反数对。

图2 复平面图

既然点是我们自己选的，那不如使最后一组相反数点对为 $\{1,-1\}$。我们取 n 等于 8 作为演示。不难看出最后选取的 8 个点均是 $x^8=1$ 的解。

图3 n=8选点示例图

对于任意 $n=2^a , a\in \mathbb{N}$，来说即为 $x^n=1$。

由欧拉公式:

可以得到公式：

所以:

上面是 $n$ 次单位复数根的推导。当 $k=1$ 时，值 $\omega_n=e^\frac{2\pi i}{n}$ 被成为主 $n$ 次单位复数根，其他的 $n$ 次单位根都是 $\omega_n$ 的幂次。其中 $\theta$ 表示为复平面单位圆上的弧长。因此 $e^\frac{2\pi i}{n}$ 表示将一个单位圆均分 $n$ 份。$n=8$ 时如下图所示。​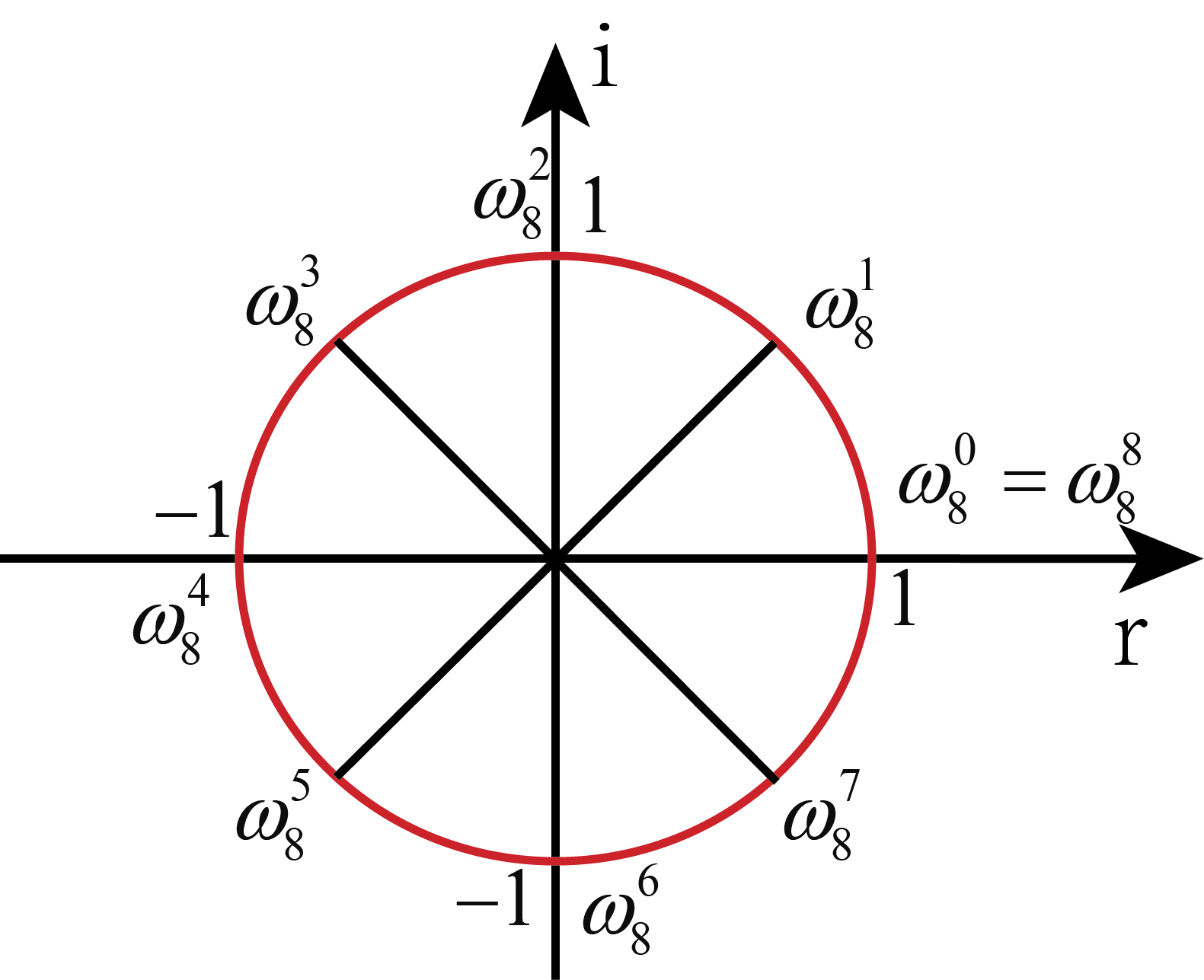图4 8次单位根示意图​

$n$ 次单位根的性质：

消去引理：

折半引理：

求和引理：

1.2 $DFT$ 与 $IDFT$

经过 1.1 节的介绍已经对多项式乘法的相关内容有了相应的了解，下面开始正式介绍 $DFT$ 与 $IDFT$，将在 1.3 节介绍 $FFT$ 与 $IFFT$ 的相关内容。我们是从多项式乘法引入的$DFT$和$IDFT$，但是$DFT$和$IDFT$的应用的场景有很多，多项式求值、大数乘法，拉格朗日插值、矩阵乘法、中国剩余定理以及环同态。

1.2.1 离散傅里叶变换（$DFT$）

设有一个 $n-1$ 次的多项式 $P(x)$:

多项式 $P(x)$ 的 $DFT$ 在单位根 $\omega_n^k = e^{2\pi i k / n} $ 上的值计算如下：

1.2.2 逆离散傅里叶变换（$IDFT$）

对 $DFT$ 过程我们可以通过矩阵进行描述 $y=Wa$：

其中 $V_n$ 是一个范德蒙矩阵，是一个可逆矩阵，因此 $IDFT$：$a=W^{-1}y$。

下面求取:$W_n^{-1}$。矩阵 $W$ 可以表示为：$W_{jk}=ω_ n^{jk}$。$W_{jk}^{-1}$ 的值应该是 $W_{jk}$ 的共轭除以 $n$。由 $\omega _n$ 的性质，我们知道 $\omega _n^k$ 的共轭是 $\omega _n^{-k}$。因此 $W_{jk}^{-1}=\frac{1}{n}ω_ n^{-jk}$。所以 $DFT$ 和 $IDFT$ 的时间复杂一致，甚至计算流程基本一致。

1.3 快速傅里叶变化（$FFT$）

其实 $FFT$ 的思路在 1.1.3 节中进行了介绍只是并不是很完善，下面进行一个较为细致的描述。详细介绍 FFT 的递归实现和迭代实现。

1.3.1 $FFT$ 递归实现

将单位根带入公式（7）得：

根据消去引理推导出得对称性以及折半引理对公式（8）进行化简。取 $k \in[0,\frac{n}{2})$ 。

即公式（9-10），这两个式子也被称为 CT(Cooley-Tukey)蝶形操作，$\omega_{n}^{k}$ 被成为转换因子。

现在给出递归版本得算法：

蝶形操作：

蝶形操作得名于其数据流图的形状，上面的推导过程出现的是 CT 蝶形变换，还有一种 GS 蝶形变换。

图5 CT蝶形操作图​

图6 CT蝶形操作简化图​

通过公式（9-10）我们可以推导出 GS 蝶形变换的形式。将公式（9）和（10）分别加减运算得：

整理得公式（11-12）不难看出，GS 操作是 CT 操作的逆过程，可以用于 $IFFT$ 中,当然也可以用在$FFT$中，通常CT方法也叫$DIT$（时域抽取）操作，GS操作也叫$DIF$（频域抽取）操作。

资源 11​

1.3.2 $FFT$ 迭代实现

继续优化。依然拿 n=8 举例。递归数据操作如图 7 所示，在递归操作中是自定向下层层展开，然后逐层向上收缩。每一次递归都会消耗堆栈资源，影响效率。如果可以从底向上计算，那么可以省去堆栈资源的消耗，提高程序运行效率。于是现在的问题就变为了如何确定递归树叶子节点的元素排序。

图8 n=8时递归示意图​

位逆序

将叶子节点元素顺序和原始元素顺序均使用二进制表示。发现二进制表示发生了左右对称反转，称之为位逆序变换。

1
2
3
4
5
//位逆序
Layer 4:	0	4	2	6	1	5	3	7
Binary:		000 100 010 110 001 101 011 111
Reverse:	000 001 010 011 100 101 110 111
Decimal:	0	1	2	3	4	5	6	7

下面是 Bit-Reverse-Copy 的实现:

函数 ReverseBits 的实现如下,基本过程就是取原值低位赋值给目标值低位，然后原值右移一位，目标值左移一位，直到循环结束。

迭代算法实现

算法 3 是$DIT$实现，算法4是$DIF$实现。$s $ 可以看作是合并轮数。$m$ 是当前合并次数下每个单元的规模。其中$\hat{1}$是乘法单位元都是$\omega_n^0$。这里的$\omega_n=e^{\pm2\pi i / n}$,在进行$FFT$操作时取正，$IFFT$操作时取负。当然IFFT还需要乘上$n^{-1}$。

下面是 n=8 时，$DIT$迭代 $FFT$ 的数据流图。

图9 n=8迭代DIT数据流图​

迭代的另一种视角

如果不对输入进行位逆序而是对输出进行位逆序应当怎样计算，下面给出一个示例算法，该算法和算法3的逻辑是类似的。只是出现了些许变动。这里的$\Phi_{rev}$是位逆序后的$\omega$的幂次表，需要注意的是这里不对输入进行位逆序而是对单位根幂次表进行位逆序。由于上述的变换，数据流图也发生了相应的改变。m表示的是当前轮次NTT的大小，n表示当前轮次CT跨度，$j_1$表示分组的起点，数据流图如图10所示，输出结果是位逆序后的。

图10 n=8迭代DIT数据流图2​

1.4 快速数论变换（$NTT$）

$FFT$ 存一些问题。首先 FFT 是在复数域上的表示，而计算机系统中表示复数，需要比实数花费更多的资源，且复数运算也比实数运算更加复杂。此外 FFT 涉及大量的正余弦运算，对于精度有影响。于是我们期望在实数域内寻找类似单位根性质的数学概念。有限域上的原根满足相应的要求。

1.4.1 数学基础

欧拉函数

欧拉函数，即 $\varphi(n)$,表示的是小于等于 $n$ 且和 $n$ 互素的数的个数。当 n 是素数时 $\varphi(n)=n-1$。

欧拉定理

对于 $a \in \mathbb{Z}$ ,$m\in \mathbb{N}^*$,若 $\gcd(a,m)=1$,则 $a^{\varphi(m)} \equiv 1 \pmod{m}$。

费马小定理

若 $p $ 为素数，$\gcd(a,p)=1$,则 $a^{p-1} \equiv 1 \pmod{p}$。

也可表达为，对于任意整数 $a $，有 $a^p \equiv a \pmod{p}$。

利用费马小定理求逆元:$a^{-1}=a^{p-2}$

阶

由欧拉定理可知，若 $\gcd(a,p)=1$，一定存在一个最小的正整数 $n$ 满足同余式 $a^n \equiv 1 \pmod{m}$。这个 $n$ 被称作 $a$ 模 $m$ 的阶记作 $\delta_m(a) $ 或者 $ord_m(a)$。具有以下性质：

性质 1：$a,a^2,\ldots,a^{\delta_m(a)}$ 模 $m $ 两两不同余，之后进入周期。

性质 2：若 $a^n \equiv 1 \pmod{m}$,则 $\delta_m(a)|n$。可以推导出若 $a^p \equiv a^q \pmod{m} $，则有 $p \equiv q \pmod{\delta_m(a)}$。

原根

给定 $n \in \mathbb{N}^*$ ，$g \in \mathbb{Z}$，满足 $\gcd(g, m) = 1$，且 $\delta_m(g) = \varphi(m)$ ，则称 $g$ 为模 $m$ 的原根。

即 $g$ 满足 $\delta_m(g)=| \mathbb{Z}_m^* |=\varphi(m)$ 。当 $m$ 是素数时，我们有 $g^i \mod m$，$0<i<m$ 的结果互不相同

原根个数：若一个数 $m$ 有原根，则它原根的个数为 $\varphi(\varphi(m))$。

原根存在定理：一个数 $m$ 存在原根当且仅当 $m=2,4,p^a,2p^a$ ，其中 $p$ 为奇素数，$a\in \mathbb{N}^*$。

原根的性质

原根具有以下性质，不难看与单位根具有类似的性质。所以可以用于替代单位根，用于简化 $DFT$ 计算。

不重性：$\forall 0 \leq i < j < \varphi(p),\ g^i \not\equiv g^j \pmod{p} $

折半性：定义 $g_n = g^{\frac{\delta_p(g)}{n}} \equiv g^{\frac{p-1}{n}}$,$g_n^k = (g_n)^k$ 则 $g_{an}^{ak} \equiv g_n^k \pmod{p}$。

对称性：$g_{2n}^{k+n} \equiv - g_{2n}^k \pmod{p}$

求和性：$\sum_{i=0}^{n-1} (g_n)^{ki} \equiv n[k=0] \pmod{p} $，$k=0$ 为真 $[k=0]=1$,否则为 $0$。

原根与模数的选择

为了实现多次二分，模数 $p$ 应选可以拆分为 $q\times 2^k +1$ 的素数,$q$ 为奇素数，$k$ 为整数,$2^k$ 模数的阶，也就是原根的最大数量。可以看下表的例子。

1.4.2 $NTT$ 的递归实现

将原根带入公式（7）得：

根据消去引理推导出得对称性以及折半引理对公式（13）进行化简。取 $k \in[0,\frac{n}{2})$ 。

简化为：

现在给出递归版本得算法,不难发现除了将单位根替换为原根，增加模运算，以及增加了参数 ，原根 $g$，模数 $p $ 外与 $FFT$ 并无太大区别。

注意NTT里的$g^{-1}$是取逆元操作，在计算$INTT$时请注意。

1.4.3 $NTT$ 的迭代实现

$NTT$ 的迭代实现同理，因此不再赘述，直接给出相应的算法。

1.5 矩阵DFT​算法

现在介绍另外一种算法，这种算法提高缓存命中率，从而提高执行效率。这种算法是将输入看作是一个行优先的矩阵进行计算，请注意对于NTT来说实际的输入指的是系数$a_i$。

如果 $n=R\cdot C$ 我们可以用 $i_r\in[0,R)$ 和 $i_c \in [0,C)$ 重写$i=i_r\cdot C+i_c$ 。这将创建一个对应 $[0,n) \backsimeq[0,R) \times[0,C)$。另一种对应关系是 $k=k_r+k_c\cdot R$ ,注意这里输出的顺序已经变成了列优先了。将$i$和$k$带入下式。

需要提前明确的一点是这里公式中$\omega$既可以是原根又可以是单位根,不过为了统一表示省去了原根的取模操作。替换可得：

将$\omega$的幂次展开：

根据原根的折半性质或者单位根的消去引理$\omega_{an}^{ak}=\omega_n^k$，可得：

则公式(14)变为如下形式：

添加一些括号来确定运算顺序则变成了：

首先对输入a子序列进行长度为$R$的$DFT$操作，然后对结果乘上旋转因子，最后进行长度为$C$的$DFT$操作。这么看可能不直观，我们将输入写成一个$R \times C$大小的矩阵：

先对对所有列进行DFT运算，然后所有元素乘上相应的转换因子，最后对所有行进行DFT运算。下面是转换转换因子矩阵$T$，注意转换因子矩阵与对列进行DFT的结果进行的是逐点相乘。因为输出是列优先排序，所以需要对结果进行一个转置，从而使得输入与输出保持同一顺序。

Four-step DFT

对上面的算法进行一个总结就是所谓的四步DFT算法,$[R \times C]$，表示为大小为$R\times C$的行优先矩阵。

$IDFT*$是省略乘上$n^{-1}$的$IDFT$，所以最后需要补上$n^{-1}$。

DFT:

  1. $[R \times C]$,对每一列进行长度为$R$的$DFT$运算。
  2. $[R \times C]$,所有元素乘上对应的转换因子$\omega^{ik}$。
  3. $[R \times C]$,对每一行进行长度为$C$的$DFT$运算。
  4. $[R \times C]$,将矩阵进行转置。

IDFT*：

  1. $[C \times R]$,将矩阵进行转置。
  2. $[R \times C]$,对每一行进行长度为$C$的$IDFT*$运算。
  3. $[R \times C]$,所有元素乘上对应的转换因子$\omega^{-ik}$。
  4. $[R \times C]$,对每一列进行长度为$R$的$IDFT*$运算。
Six-step DFT

对列进行操作，无法读取连续的内存会影响计算效率，可以增加转置操作，于是获得六步DFT算法：

DFT:

  1. $[R \times C]$,将矩阵进行转置。
  2. $[C \times R]$,对每一行进行长度为$R$的$DFT$运算。
  3. $[C \times R]$,将矩阵进行转置。
  4. $[R \times C]$,所有元素乘上对应的转换因子$\omega^{ik}$。
  5. $[R \times C]$,对每一行进行长度为$C$的$DFT$运算。
  6. $[R \times C]$,将矩阵进行转置。

IDFT*:

  1. $[C \times R]$,将矩阵进行转置。
  2. $[R \times C]$,对每一行进行长度为$C$的$IDFT*$运算。
  3. $[R \times C]$,所有元素乘上对应的转换因子$\omega^{-ik}$。
  4. $[R \times C]$,将矩阵进行转置。
  5. $[C \times R]$,对每一行进行长度为$R$的$IDFT*$运算。
  6. $[C \times R]$,将矩阵进行转置。

2 NTT 设计

本节主要是介绍对NTT的设计，例如模约简方案、转置优化以及预计算。最后探讨有哪些可以进行的优化。

2.1 模约简

2.1.1 朴素方案

在模数约简的朴素方法中，如果硬件支持的话，会使用一个硬件指令将两个字（word）长度的被除数除以一个字长度的除数，得到一个字长度的商和一个字长度的余数。如果硬件不支持这种指令，那么就需要在软件中模拟这种指令。

这样的指令在x86和x86-64架构中是存在的。对于软件模拟，GNU GCC和Clang编译器在32位平台上提供了uint64_t类型，在64位平台上提供了unsigned __int128类型，并且这些类型都支持除法操作。

2.1.2 Barrett 约简

巴雷特约简的思路很简单，将计算$z =a \mod p$，转换为$z=a- tp,t=\lfloor ap^{-1}\rfloor$ 。于是问题就从模运算转换为了求取$p^{-1}$的近似值,也就是$t$的近似值。

对$t$进行进行变换：

其中$b$是基底，计算机系统中通常使用二进制表示，即$b=2$，$k$是模数相对于基底的位宽$k=\log_{b}p+1$，之所以是$b^{2k}$是因为通常运用模约简的场景是模乘，因此$a\in[0,p^2)$。经过变换，我们发现分离出来一个一个仅和模数有关的量:$\alpha = \frac{b^{2k}}{p}$，这意味着对同一模数的约简可以提前计算$\alpha$，其他部分可以通过右移和乘法完成，乘法运算效率显著高于除法运算，位移效率更快，计算速度提升了很多。

为了避免浮点数计算，令$\beta=\lfloor \frac{b^{2k}}{p} \rfloor$,替换掉$\alpha$,得到$t$的近似$\hat{t}$：

现在考虑$t$与$\hat{t}$的误差：

且$0 \le \lambda \lt 1$,$0 \le \mu \lt 1$，此外还有：

因为$a\lt b^{2k}$,所以$\lfloor \frac{a}{b^{k-1}} \rfloor \leq b^{k+1}-1$；又因为$p \ge b^{k-1}$,所以$\lfloor \frac{b^{2k}}{p}\rfloor \leq b^{k+1}$。对上面不等式放缩：

又因为$\hat{t} \le t$,所以可得：

近似性不错，进一步可得：

又因为$a-tp=z\lt p$，所以：

不难看出使用近似方法得出得值有可能比p大，但是通过最多两次减法就可以修正误差，下面给出完整的算法：

$z_1$和$z_2$的运算可以通过位与操作直接去掉k位的高位即可，简化了计算。下面给出$\beta$的算法：

2.1.3 Montgomery 约简

蒙哥马利模乘约减的思路是通过变换，将需要取模的数控制到很小的范围（$[0,(p-1)^2] \rightarrow [0,2p-1]$ ）然后通过少量减法获取最后结果。并通过位运算简化计算，例如：右移除法、位与取模。

蒙哥马利约简

对于$\forall t \in \mathbb{Z}$且满足$a < r p$，$r\gt p$，$\gcd(r,p)=1$ 。$p$是以$b$为基底,长度为$k$的整数，则r的取值为$b^k$，计算机中$b$为$2$，显然$r\gt p$。但是只有当$\gcd(b,p)=1$时才满足$\gcd(r,p)=1$，之前提到的格式是满足条件的。

由于$r$和$p$互素，所以存在$r’,p’ \in[0,p)$使得下式成立，$r’$是$r$在$p$下的逆元 ，$p’$是$p$在$r$下的负逆元。

于是：

其中$\lfloor \frac{ap’}{r} \rfloor r+(ap’ \bmod r)$是将$ap’$表达为成商乘上除数加余数的形式。上面的推导过程将对$ar’$模$p$转换为了对$\frac{a+((a\bmod r)p’ \bmod r)p}{r}$模$p$操作。显然$((a\mod r)p’ \mod r)p \lt rp$又因为$a < r p$所以可得下面的关系，不难发现最多只需一次减法就可以完成取模操作，其中模$r$可以通过位与运算，除$r$可以通过位右移运算完成，之所以做两次模$r$运算是为了降低乘法位宽。

下面给出相应的算法：

蒙哥马利域

由上面蒙哥马利约简的过程不难发现实际是对$xR^{-1}$(这里的$R^{-1}$就是上面提到的$r’$,只是为了方便区分)进行约简，所以在使用蒙哥马利约简时，首先需要转换到蒙哥马利域中，蒙哥马利域中的形式表示为$\bar{x}$，转换入蒙哥马利域的方式：

显然，转入蒙哥马利域的成本是高昂的，只有在蒙哥马利域内计算值得时才会使用蒙哥马利约简，在蒙哥马利域中加法和减法（结合律）不受影响。

但是蒙哥马利域上的乘法是不正确的，这里蒙哥马利域中的乘法用 $\times$表示，正常的乘法用$\cdot$表示。我们期望的结果是：

但是实际上如果直接相乘获得结果如下：

蒙哥马利域上的乘法定义如下：

最后就是蒙哥马利域的转出，转出如下所示。

蒙哥马利模乘

在执行蒙哥马利乘法本身开销并不高，但是需要完成一些提前计算，这些计算的开销较高。

  • 蒙哥马利域的转入
  • $p’$的计算
  • 蒙哥马利域的转出

在约简过程中已经完成了蒙哥马利域的转出。p’的计算可以通过扩展欧几里得算法获得。对于转入还存在另一种策略：

第二种策略策略是省去模p的运算，但是失去了乘R位运算优势，取而代之的是乘上$R^2 \mod p$，可以提前计算，并需要执行约简操作，因为取模开销很大，大概率第二种策略效率更高一点。于是蒙哥马利模乘可以表示如下：

2.1.4 小结

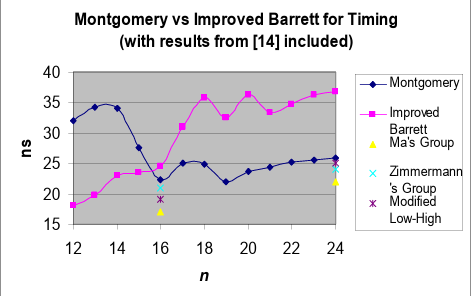
上面介绍了三种模约简方法，模约简主要用于模乘中，这里主要对比分析一下巴雷特和蒙哥马利，至于朴素方案效率太低就不分析了。在FPGA上当一次处理位宽大于$16$-bit时蒙哥马利更具有优势，反之巴列特算法有优势。对CPU或者GPU版本没有看到相应的资料，不过从两种算法从时间复杂度上是类似的。连续模乘可能蒙哥马利的优势更大。

图 11 FPGA蒙哥马利与巴雷特对比​

2.2 root power 预计算

算法3中需要反复执行$\varphi=\varphi \omega_m$，这里的m是当前合并轮次下每个单元的数据规模或者是蝶形运算的步长，$s $ 可以看作是当前合并轮数，$n$是输入规模，$l$是总的轮数。$\omega_m=\omega^{2^{n-s}}$,$s=\log_2m$。一共具有两种预计算方案

方案一： 预计算$\omega$的幂到一个root power表$t$中，即$t[i]=\omega^i ,i\in[0,\frac{n}{2})$。对于给定的$j$和$m=2^s$，我们可以表示旋转因子$\varphi =t[j\cdot 2^{\alpha }], \alpha =n-s,j\in [0,2^{s-1})$。

方案二： 计算每个粒度$s\in[1,n]$,单独的root power表：

记$T_n=t$，$\sum_{s=1}^n|T_s|=\sum_{s=1}^n 2^{s-1}=2^n-1$。对于给定的$j$和$m=2^s$，我们可以表示旋转因子$\varphi =T[j]$。然后我们将将所有的$T_s$组成一个大的表$T$。

对于给定的$j$和$m=2^s$，我们可以表示旋转因子$\varphi =T[\beta + j],\beta=2^{s-1}-1=\frac{m}{2}-1$。

两种方式$T[\beta+j]$ 和$t[j \cdot 2^\alpha ]$，内层索引都是相同的，$\alpha$ 和 $\beta$表示循环中不变的表达式，在循环开始前计算一次。但是$T$，可以使用指针指向$T[\beta]$,

一步解引用。而$t$需要先位移后解引用。

Four-step算法： 因为要用到所有的幂次，所以直接预计算所有的幂次，构建幂次表$T_$即可。需要设计合适的索引。我的想法是利用折半引理，在对行或是对列的NTT中索引格式只需要在方案二的基础上进行细微改动即可，只需要乘上总规模$N$除当前NTT规模$n$的商即可，$T_[(\beta+j)\frac{N}{n}]=T_*[\beta \mu+j\mu]$,只是这种方法会使得方案本一步完成的解引用，需要两步而且增加的是开销较高的乘法。至于列运算结束后的旋转因子矩阵直接按照输入索引去查询即可，因为输入矩阵和旋转因子因子矩阵是一一对应的。

2.3 转置优化

矩阵的转置有两种方式一种是out-place,一种是in-place。前者需要申请一块同等大小的空间，从而完成转置，即空间复杂度$O(R\times C)$。后一种，空间复杂度远小于$O(R\times C)$。这里主要讨论in-place转置方案，对于方阵很简单只需要交换$$与$$处的元素即可。

下面讨论$n\times cn$形式的矩阵转置，为了方便表示不妨取$c=2$。将一个$n\times 2n$的矩阵$M$拆分成两个$n\times n$的方阵$A$和$B$:

则转置表达为：

定义$\phi(M)$:

现在将两个子矩阵$A^T$，$B^T$的行用向量表示：

所以我们可以通过某种方法$\rho$重新排列$\phi(M)$的索引，使其等于$M^T=\rho \phi(M)$，对于索引$i$的目标位置$j$满足：

下面探究对于列排布能否实现同样的作用， 首先我们定义对方阵的行进行索引重排为$\rho_r$,对其列进行索引成排为$\rho_c$。很明显对于一个矩阵A,满足一下关系：

我们已经证明:

现在令$M=\rho_c N$,即可获得：

现在证明对列进行排布同样可以完成相应的操作，只不过要现在哎方阵转置前进行列排布。对列进行排布对那内存更友好，需要$O(2n)$的额外空间。

对于$cn\times n$形式的矩阵，只需要对列执行$\rho^{-1}$然后对方阵转置就行。

2.4 可能的优化

2.4.1 位逆序省略

我们回到最开始，我们引入DFT是为了进行多项式乘法：

如果使用$DIF$完成$DFT$，使用$DIT$完成$IDFT$，我们就可以省略$DIF$最后的位逆序，以及$DIT$最开始的位逆序，紧挨着的两个位逆序可以省略。

2.4.2 省略转置

矩阵算法省略转置的原理与位逆序省略的原理相同，如果连续做$DFT$和$IDFT$，我们可以省略$DFT$最后的转置以及$IDFT$最开始的转置。

2.4.3 合并

  1. 可以将对列之后乘旋转因子的操作合并到对列操作或者对行操作中，这样可以减少内存读写的次数。
  2. 对于$IDFT$可以将乘以$n^{-1}$,合并到四步$IDFT*$中，例如乘旋转因子的过程中。

参考文献

[1]七海. 基础知识：FFT - 简单入门[EB/OL]//七海の参考書. (2021-03-29)[2024-01-21]. https://shiraha.cn/2021/The-concept-of-fft-introducing-edition/.

[2]快速数论变换（NTT）及蝴蝶操作构造详解[EB/OL]//知乎专栏. [2024-01-21]. https://zhuanlan.zhihu.com/p/80297169.

[3]Frigo M, Leiserson C E, Prokop H, et al. Cache-oblivious algorithms[J]. ACM Transactions on Algorithms (TALG), 2012, 8(1): 1-22. https://doi.org/10.1145/2071379.2071383.

[4]LESAVOUREY A, NEGRE C, PLANTARD T. Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications[C/OL]//ICETE: International Joint Conference on e-Business and Telecommunications: 4 [SECRYPT]. Lisbon, Portugal, 2016: 368-375[2024-02-28]. https://hal.science/hal-01330898. DOI:10.5220/0005998503680375.

[5]Finite Field Implementations[Z/OL]. [2024-01-26]. https://docs.google.com/presentation/d/1I5QS58LtA3iiiPiVHHcN7oufCoo8sIDh9UvnJHWjA2Q.

[6]RISC ZERO. Finite Field Implementations: Barrett & Montgomery[Z/OL]. (2023-02-17)[2024-01-26]. https://www.youtube.com/watch?v=hUl8ZB6hpUM.

[7]AGARWAL R C, COOLEY J W. Fourier transform and convolution subroutines for the IBM 3090 Vector Facility[J/OL]. IBM Journal of Research and Development, 1986, 30(2): 145-161. DOI:10.1147/rd.302.0145.

[8]董晓算法. G41 快速傅里叶变换 FFT算法 多项式乘法_哔哩哔哩_bilibili[EB/OL]. [2024-01-21]. https://www.bilibili.com/video/BV1Le4y1V78D/.

[9]董晓算法. G43 快速数论变换 NTT算法_哔哩哔哩_bilibili[EB/OL]. [2024-01-21]. https://www.bilibili.com/video/BV1a3411Z7vL/.

[10]HEIDEAN M, JOHNSON D, BURRUS C. Gauss and the history of the fast fourier transform[J/OL]. IEEE ASSP Magazine, 1984, 1(4): 14-21. DOI:10.1109/MASSP.1984.1162257.

[11]COHEN H, FREY G, AVANZI R, 等. Handbook of Elliptic and Hyperelliptic Curve Cryptography[M/OL]. 0 版. Chapman and Hall/CRC, 2005[2024-02-26]. https://www.taylorfrancis.com/books/9781420034981. DOI:10.1201/9781420034981.

[12]Hardcaml Zprize[EB/OL]. [2024-01-30]. https://zprize.hardcaml.com/ntt-top-level.html.

[13]IEEE Xplore Full-Text PDF:[EB/OL]. [2024-02-28]. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4176858.

[14]Math & Engineering[EB/OL]. [2024-02-22]. https://xn—2-umb.com/.

[15]LIANG Z, ZHAO Y. Number Theoretic Transform and Its Applications in Lattice-based Cryptosystems: A Survey[M/OL]. arXiv, 2022[2024-01-30]. http://arxiv.org/abs/2211.13546.

[16]KNAUTH C, ADAS B, WHITFIELD D, 等. Practically efficient methods for performing bit-reversed permutation in C++11 on the x86-64 architecture[M/OL]. arXiv, 2017[2024-01-29]. http://arxiv.org/abs/1708.01873.

[17]DUPAQUIS V, VENELLI A. Redundant Modular Reduction Algorithms[C/OL]//PROUFF E. Smart Card Research and Advanced Applications. Berlin, Heidelberg: Springer, 2011: 102-114. DOI:10.1007/978-3-642-27257-8_7.

[18]Knezevic M, Vercauteren F, Verbauwhede I. Speeding up Barrett and Montgomery modular multiplications[J]. IEEE Transactions on Comput, 2009, 2.bar_mont.pdf (kuleuven.be)

[19]KRAPIVENSKY V. Speeding up decimal multiplication[M/OL]. arXiv, 2020[2024-01-21]. http://arxiv.org/abs/2011.11524. DOI:10.48550/arXiv.2011.11524.

[20]LONGA P, NAEHRIG M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography[A/OL]. (2016)[2024-01-30]. https://eprint.iacr.org/2016/504.

[21]REDUCIBLE. The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?[Z/OL]. (2020-11-15)[2024-01-21]. https://www.youtube.com/watch?v=h7apO7q16V0.

[22]LONGA P, NAEHRIG M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography[A/OL]. (2016)[2024-07-11]. https://eprint.iacr.org/2016/504.

‍

‍